Brief Background of Piezoelectricity
In 1880, Pierre and Jacques Curie reported the first experimental results demonstrating the piezoelectric effect, using specially prepared crystals, such as quartz, tourmaline, cane sugar, and Rochelle salt. Mechanical stress on these crystals successfully induced a surface charge, later, this was called the “the direct piezoelectric effect”, which illustrates electrical charge generation based on applied mechanical stress. In contrast to direct piezoelectricity, converse piezoelectricity demonstrates a phenomenon wherein the application of an electrical field creates mechanical strain. In 1881, Lippman mathematically proved the converse piezoelectric effect, using fundamental thermodynamic principles: the Curie’s quickly confirmed this effect. Quantitative proof of the complete reversibility of electro-elasto mechanical deformations in piezoelectric crystals was also later obtained [3].
In crystallography, combinations of symmetry elements that can compatibly pass through a common point are called point groups, and only 32 non-identical point groups are possible [4]. The structural symmetry of a crystal geometrically affects its structural and physical properties, for instance, its dielectric, elastic, piezoelectric, thermal and optic properties, etc. The 32 point groups can be categorized into 11 centrosymmetric types and 21 non-centrosymmetric types. A crystal with a symmetric center does not show any third rank tensor properties such as piezoelectricity, dijk. Among these crystals, 20 exhibit finite piezoelectric effects and 10 have only one unique polar direction. Along the unique axis, a polarity is obtained with finite pyroelectric effects. When the equilibrium spontaneous polarizations exist and can be reoriented by an external electric field with sufficient strength, these materials are termed ferroelectric [5,6,7].
The application of stress on a non-centrosymmetric crystal exhibits a movement of the positive and negative ions with respect to each other, generating an electric charge difference at the surface of the material. This is the generator action through which we obtain the direct piezoelectric effect: the conversion of mechanical energy into electrical energy [8]. In contrast, when an electric field is applied to a crystal, either a compressive or tensile strain is produced in the material, depending on the direction of the field and the size of the respective piezoelectric coefficients. This motion is the actuator or motor action through the converse piezoelectric effect: the conversion of electrical energy into mechanical energy.
Ferroelectricity can exist in a number of crystal structures and compositions within those structures. One of the most important structures is perovskite. Perovskite is the name of the mineral calcium titanate (CaTiO3), a non-ferroelectric material. Most of the useful piezoelectric and ferroelectric ceramics, such as barium titanate, (BaTiO3) potassium niobate (KNbO3), and lead titanate (PbTiO3) have perovskite-type structures. These oxide ceramics have the general formula ABO3, where O represents oxygen, A represents a cation with a larger ionic radius in twelve-fold coordination, and B represents a cation with a smaller ionic radius in octahedral six-fold coordination. Figure 1 shows a cubic ABO3 perovskite-type unit cell.
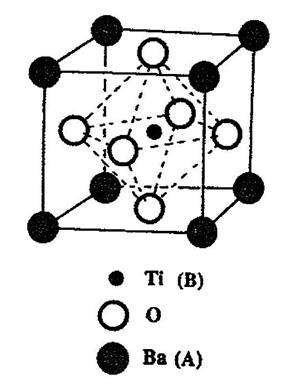
Figure 1. A cubic ABO3 perovskite-type unit cell.
The first piezoelectric ceramic with perovskite is barium titanate, which shows anomalous dielectric properties. Other materials such as PbTiO3, KNbO3 and (K,Na)NbO3 have also been studied for their piezoelectric applications in single crystal and polycrystalline form [5]. The performance of these materials, however, is insufficient for practical applications. The discovery of lead zirconate titanate (Pb(ZrxTi1-x)O3) ceramics by Jaffe et al. in 1954 led to the wide usage of piezoelectricity possible in polycrystalline materials. This composition is adjacent to the morphotropic phase boundary (MPB). The MPB compositions have relatively temperature-independent phase boundaries between ferroelectric phases and high symmetric phases. The polycrystalline solids can be easily poled due to the large number of polarization directions that can be utilized. Moreover the phase boundary reduces anisotropy energy, which reduces domain wall energy and thus increases wall mobility. In turn, this provides a high extrinsic domain wall contribution to electromechanical properties [9].
A variety of compositional modifications of PZT-based ceramics have been made to enhance and to optimize dielectric and piezoelectric properties for specific applications. PZT ceramics can be categorized into two groups: ‘hard’ and ‘soft.’ Generally, acceptor ions make ‘hard’ PZTs, which have a small displacement at off-resonance strain, but a large strain with a resonance condition, low dielectric loss, and high mechanical quality factor (Qm = 1/tan?m). They are suitable for ultrasonic applications, such as ultrasonic welders and ultrasonic motors. On the other hand, ‘soft’ PZTs present a large strain at off-resonance, a high dielectric loss, and a low mechanical quality factor. Off-resonance devices, such as multi-layer actuators, are the main applications for these materials. Further modifications can be made to manipulate the transition of the ferroelectric phases, in order to enhance electromechanical properties, but this results in increased loss and temperature dependence.
...from thesis of Dr. Seung Ho Park, The Pennsylvania State University (2007)
References
1. K. Uchino, J. R. Giniewicz: Micromechatronics (Marcel Dekker, New York, 2003)
2. K. Uchino, J. Zheng, A. Joshi, Y.H. Chen, S. Yoshikawa, S.Hirose, S. Takahashi and J.W. C. DE Vries: J. Electroceram. 2 (1998) 33.
3. B. Jaffe, J.W. Cook, and H. Jaffe, Piezoelectric Ceramics, Academic Press (1971)
4. F. D. Bloss, Crystallography and crystal chemistry (Holt, Rinehard and Winston, Inc. 1971)
5. Y. Xu, Ferroelectric materials and their applications (Elsevier Science Publishers 1991 New York)
6. R.C. Buchanan, Ceramic Materials for Electronics, New York, Marcel Dekker, Inc. (1991)
7. G. H. Haertling, Journal of American Ceramic Society, 82, (1999) 797
8. A. J. Moulson and J. M. Herbert, Electroceramics, Cambridge, University Press (1990)
9. C. A. Randall, A. Kelnberger, G. Y. Yang, R. E. Eitel and T. R. Shrout: Journal of Electroceramics, 14 (2005) 1777
